并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

并查集最常用的两种操作

- 合并（Union）:把两个不相交的集合合并为一个集合
- 查询（Find）：查询两个元素是否在同一个集合中

下面我们通过一道模板题来讲解并查集的用法

（洛谷P1551）亲戚 题目背景 若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。 题目描述 规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。 输入格式 第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。 以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。 接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。 输出格式 P行，每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

  • 样例输入 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    6 5 3
    1 2
    1 5
    3 4
    5 2
    1 3
    1 4
    2 3
    5 6

  • 样例输出 

    1
    2
    3
    Yes
    Yes
    No

并查集初始化

并查集初始化的重要思想在于，用集合中的一个元素代表集合

并查集初始化，将每个元素的父亲节点设为自己：

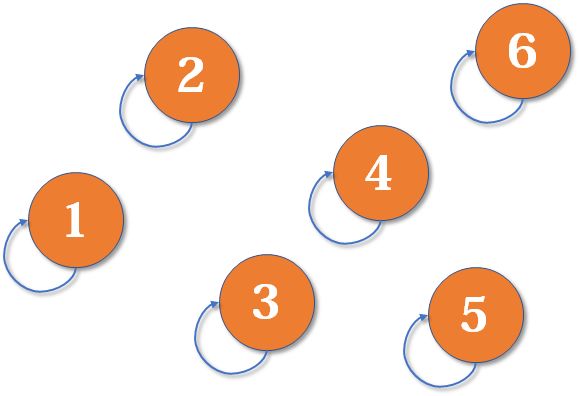
  • 初始状态 
    1
    2
    3
    for(int i = 1;i <= n;++i){
        t[i] = i;
    }
    或者 
    1
    2
    3
    4
    5
    for(int i = 1;i <= n;++i){   //结构体实现
        t[i].date = i;          //该集合的数据
        t[i].rank = 0;          //该集合的秩
        t[i].parent = i;   //该集合的父亲节点   
    }

合并操作

接下来就是喜闻乐见的合并操作了 >tips：在普通的集合合并中，谁当老大（父亲节点）并不重要，只需要有一个元素能够代表整个集合就可以了

  • 1、3合并:

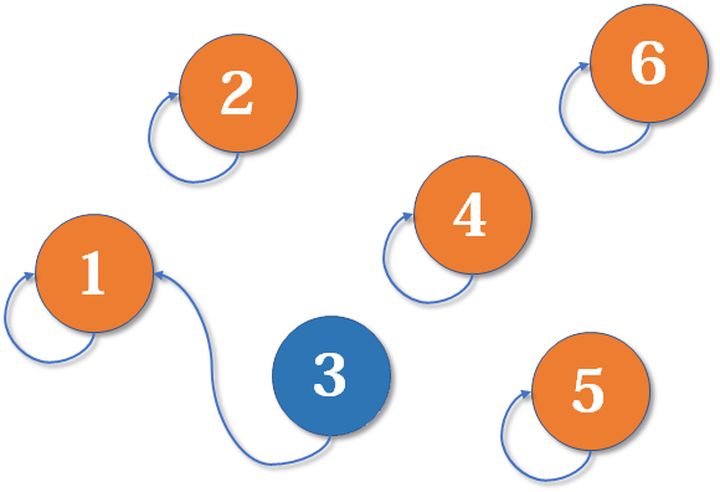
  • 1、2或者2、3合并:

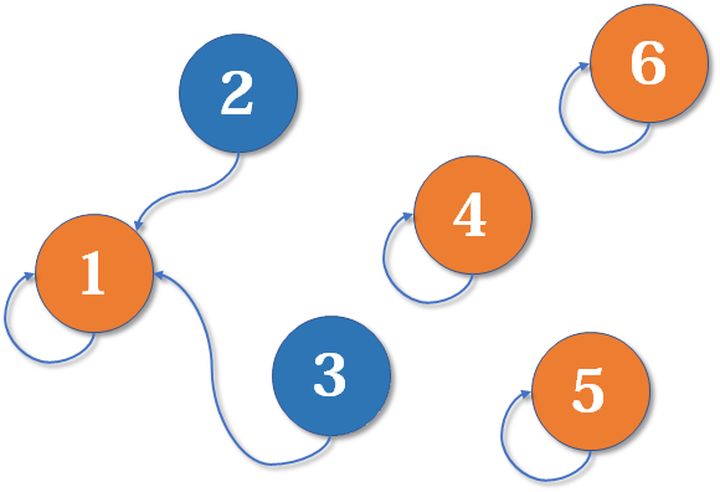
  • 4、5、6合并:

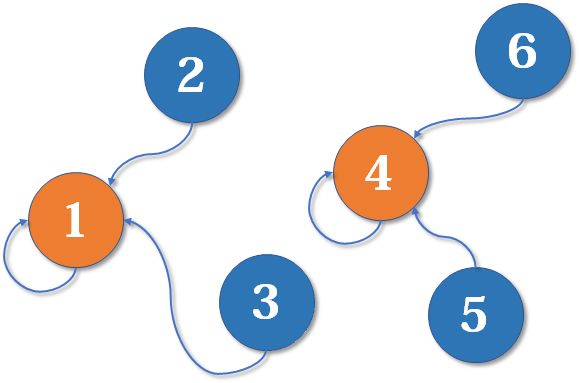
  • 1、4合并:

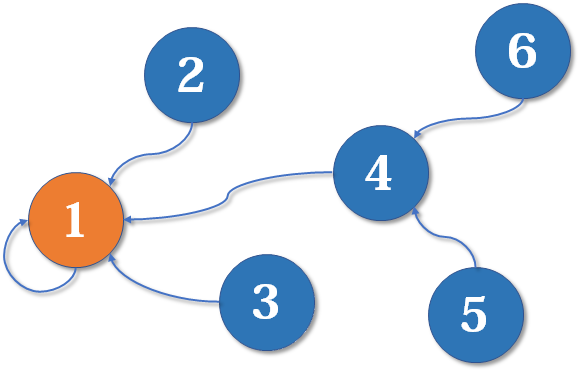
  • 树状结构:

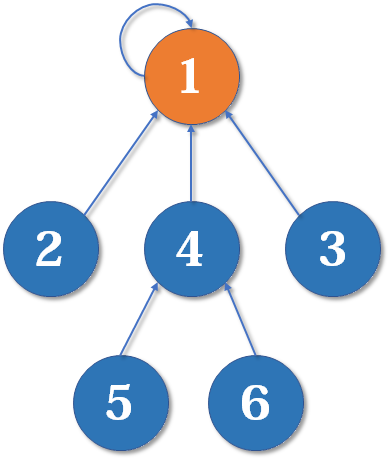
这样的结构里面，我们要寻找一个集合的代表元素（父亲节点），只需要通过集合中任意一个元素，然后一层一层往上访问父节点，直达树的根节点（橙色的圆）即可。根节点的父节点就是他自己。（我的老大是我自己）

通过这种方法我们可以实现代码（最简单的并查集代码）: - 查询: 

1
2
3
4
5
6
7
8
int Find_Set(ll x){ 
    if(t[x]!=x){
        return Find_Set(t[x]);     
    }
    else{
        return x;
    }
}
或者 
1
2
3
4
5
6
7
8
int Find_Set(USFTree t[],int x){    //结构体实现
    if(t[x].parent != x){
        return Find_Set(t,t[x].parent);
    }
    else{
        return x;
    }
}
用递归的的方法查询代表元素（父亲节点），要判断两个元素是否属于同一个集合，看他们的父亲节点是否同一个即可:

  • 合并: 
    1
    2
    3
    4
    5
    6
    void Union_Set(ll x,ll y){
        x = Find_Set(x);
        y = Find_Set(y);
        t[x] = y;
        return ;
    }
    或者 
    1
    2
    3
    4
    5
    6
    void Union_Set(USFTree t[],int x,int y){    //结构体实现
        x = Find_Set(t,x);
        y = Find_Set(t,y);
        t[x].parent = y;
        return ;
    }
    合并操作只需要找到两个集合的代表元素（父亲节点），把前者的父亲节点设为后者即可（此方法并不是最优化合理的方法，下文给出更合理的方法）:

路径压缩

上面最简单的并查集方法效率是比较低的，比如这个集合:

随着整个链表越来越长，我们查询集合代表元素（父亲节点）就会越来越困难，要做的操作次数越来越多，从而导致效率变低。

这个时候我们只需要在查询父节点的时候让集合的每个元素的父节点都指向集合的祖先节点（代表元素）大概率就类似菊花图一样的结构

  • 代码实现: 
    1
    2
    3
    4
    5
    6
    7
    8
    int Find_Set(ll x){ 
        if(t[x]!=x){
            return t[x] = Find_Set(t[x]); //按祖先结点维护
        }
        else{
            return x;
        }
    }
    或者 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    int Find_Set(USFTree t[],int x){
        if(t[x].parent != x){
            t[x].parent = Find_Set(t,t[x].parent)；
            return t[x].parent; //按祖先结点维护、结构体实现
        }
        else{
            return x;
        }
    }
    通常简写一行 
    1
    2
    3
    int Find_Set(ll x){ 
        return t[x]==x ? x : (t[x]=Find_Set(t[x]));
    }
    >要注意赋值运算符：“=” 的优先级没有三元运算符："?" 高，所以这里要加括号

为什么要用三元运算符而不用 if 语句?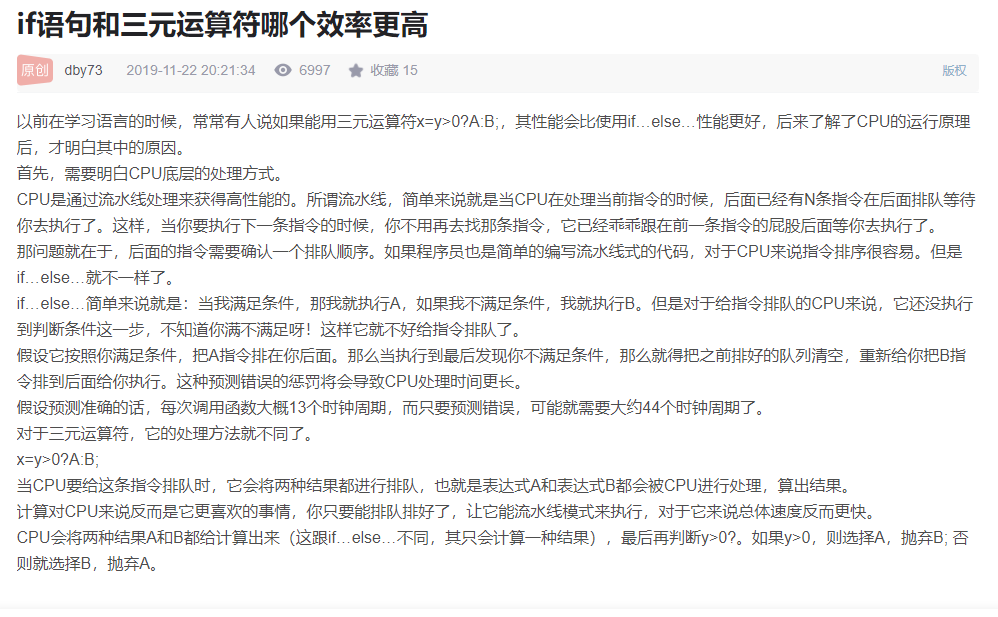

按秩合并

由于路径压缩只会在查询操作的时候进行，并且也只是压缩一条路径，所以并查集最终的结构可能还是会很复杂

例:

我现在有两个集合，一个高度比较矮，一个高度比较高，我需要将他们合并

  • 合并前:
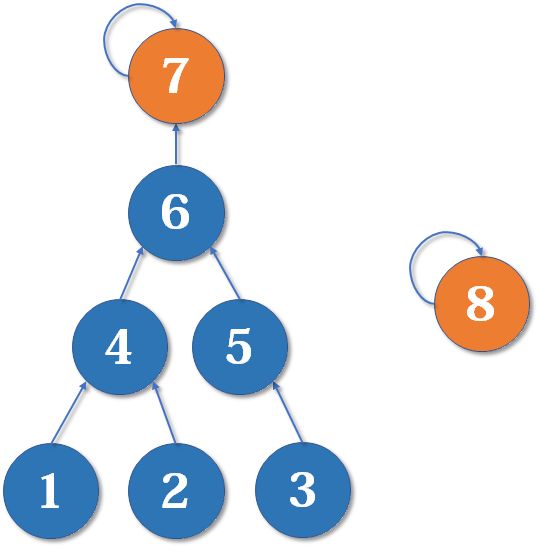
  • 合并后:

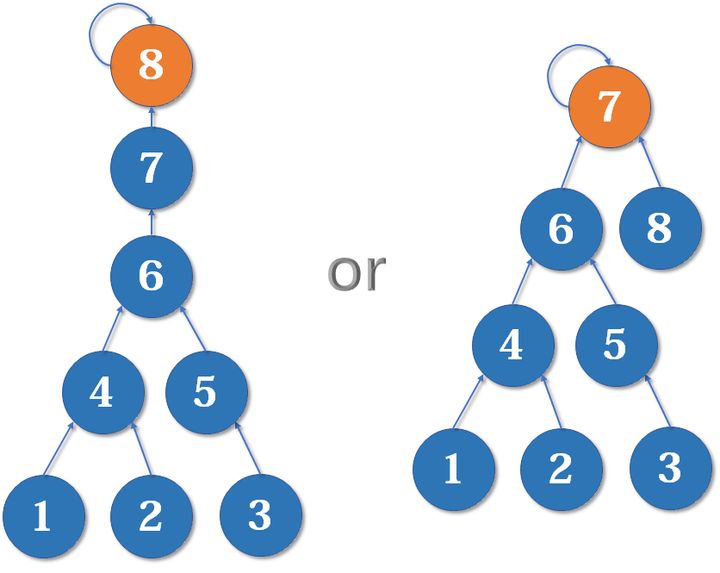
很明显，左边的集合树的高度明显比右边的高，进行查询操作的时候效率肯定会更慢一些

因此，得出结论，我们应该把简单的树往复杂的树上合并，而并不是相反，这样我们查询集合元素的父亲节点时访问的层数可以更少而不是更多

用一个 rank[] 数组记录每个集合的秩（树的高度），开始先将所有集合的秩初始化为1，就跟初始化并查集一样。合并的时候比较两个集合的秩，将rank较小的往rank较大的身上合并

  • 代码实现: 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void Union_Set(ll x,ll y){
        x = Find_Set(x);
        y = Find_Set(y);
        if(x==y){
            return; // 如果两个元素的祖先节点相同，说明在同一个集合中
        }
        if(rankSiz[x]>rankSiz[y]){ //按秩维护
            swap(x,y); // 默认x元素的rank比y元素的rank小反之则交换x与y
        }
        t[x] = y;
        rankSiz[y] += rankSiz[x];
    }
    或者 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    void Union_Set(USFTree t[],int x,int y){    //结构体实现
        x = Find_Set(t,x);
        y = Find_Set(t,y);
        if(x==y) return;
        if(t[x].rank>=t[y].rank){
            t[y].parent = x;
            t[x].rank++;
        }
        else{
            t[x].parent = y;
            t[y].rank++;
        }
    }

（洛谷P1551）亲戚AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <algorithm>
#include <windows.h>
#define ll long long
using namespace std;
ll n,m,p,x,y;
ll t[20000],rankSiz[20000];

int Find_Set(ll x){ 
    return t[x]==x ? x : (t[x]=Find_Set(t[x]));
    // if(t[x]!=x){
    //     return t[x] = Find_Set(t[x]); //按祖先结点维护
    // }
    // else{
    //     return x;
    // }
}

void Uniom_Set(ll x,ll y){
    x = Find_Set(x);
    y = Find_Set(y);
    if(x==y){
        return; // 如果两个元素的祖先节点相同，说明在同一个集合中
    }
    if(rankSiz[x]>rankSiz[y]){ //按秩维护
        swap(x,y); // 默认x元素的rank比y元素的rank小反之则交换x与y
    }
    t[x] = y;
    rankSiz[y] += rankSiz[x];
}

int main()
{
    cin >> n >> m >> p;
    for(int i = 1;i <= n;++i){
        t[i] = i;
        rankSiz[i] = 1;
    }
    for(int i = 1;i <= m;++i){
        cin >> x >> y;
        Uniom_Set(x,y);
    }

    for(int i = 1;i <= p;++i){
        cin >> x >> y;
        Find_Set(x)==Find_Set(y) ? cout << "Yes" << endl : cout << "No" << endl;
    }
    system("pause");
    return 0;
}

凡是涉及到元素的分组管理问题，都可以考虑使用并查集进行维护！

参考链接